Sorting Algorithms Explained

There are various types of sorting technique which offers different speeds for different types of initial data arrangements. I am not about to sit down here and type a length narrative explaining how each of them functions. Better yet, I will let the animated GIF do the talking.

The resources (like the animated gifs, codes, pseudocode, algorithm) in this webpage do not belong to me. The credit goes to all the hardworking developers and publishers which is listed my my Reference list below.

Bubble Sort

Example 1

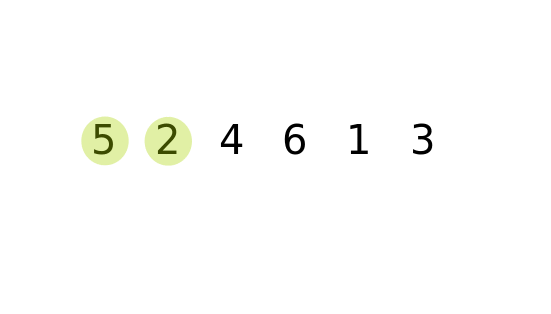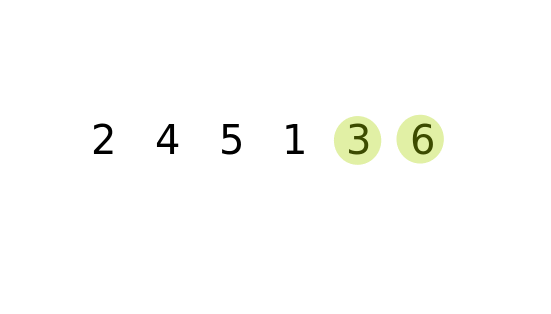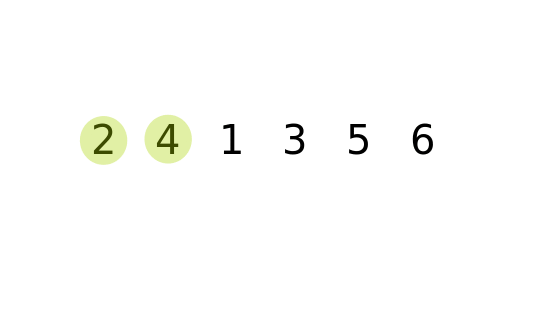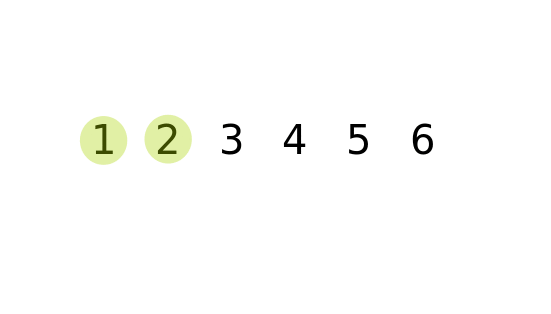
Example 2

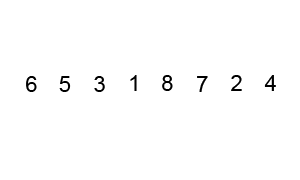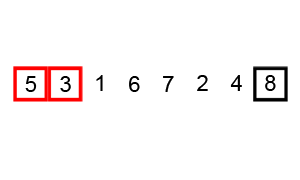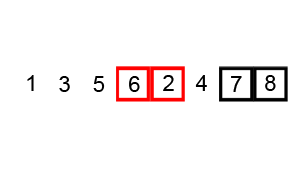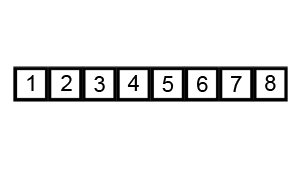
Key Notes
– Bubble sort takes Ο(n²)

Algorithm

Step 1 - Starts with very first two elements (i=0 and i+1), comparing them
         to check which one is greater.
Step 2 - Swap the elements keeping smaller elements on the left-hand side
         of the array
Step 3 - Add i++
Step 4 - Compare the next two elements (i and i+1) and swap the elements if
         the left-hand side element is greater than the right-hand side.
Step 5 - Continue until end of the array
Step 6 - Repeat again from index 0 until list is sorted

Pseudocode

procedure bubbleSort( list : array of items )
   loop = list.count;

   for i = 0 to loop-1 do:
      swapped = false

      for j = 0 to loop-1 do:
         /* compare the adjacent elements */
         if list[j] > list[j+1] then
            /* swap them */
            swap( list[j], list[j+1] )
            swapped = true
         end if
      end for

      /*if no number was swapped that means
      array is sorted now, break the loop.*/
      if(not swapped) then
         break
      end if

   end for
end procedure return list

Example Code in C#

public void BubbleSort(int[] intArray)
{
	Console.WriteLine("==Unsorted Array Input==");
	for (int i = 0; i < intArray.Length; i++) { Console.WriteLine(intArray[i]); } for (int i = intArray.Length - 1; i > 0; i--)
	{
		for (int j = 0; j <= i - 1; j++) { if (intArray[j] > intArray[j + 1])
			{
				int highValue = intArray[j];

				intArray[j] = intArray[j + 1];
				intArray[j + 1] = highValue;
			}
		}
	}

	Console.WriteLine("==Sorted Array Using Bubble Sort==");
	for (int i = 0; i < intArray.Length; i++)
	{
		Console.WriteLine(intArray[i]);
	}
}

Output

==Unsorted Array Input==
100
15
11
12
10
-1
0
==Sorted Array Using Bubble Sort==
-1
0
10
11
12
15
100

Insertion Sort

Key Notes
– Average and worst case complexities are of Ο(n²), where n is the number of items
– Uses nested looping

Example 1

Example 2

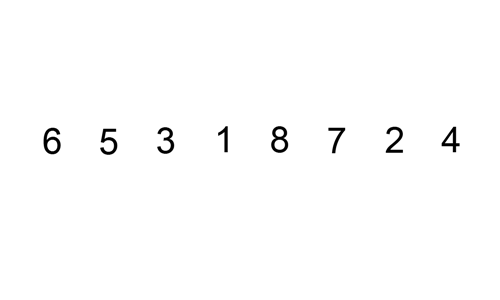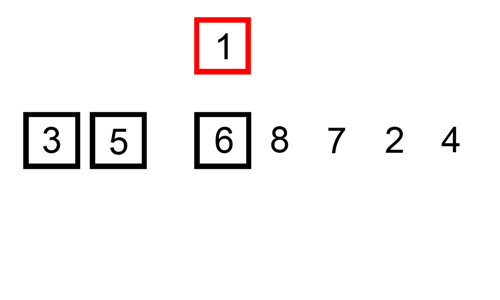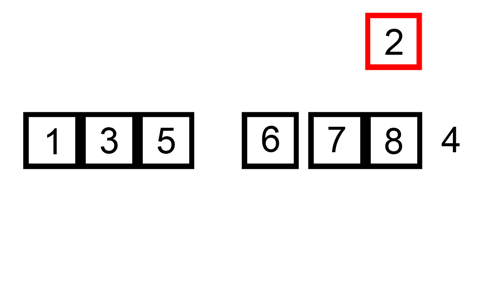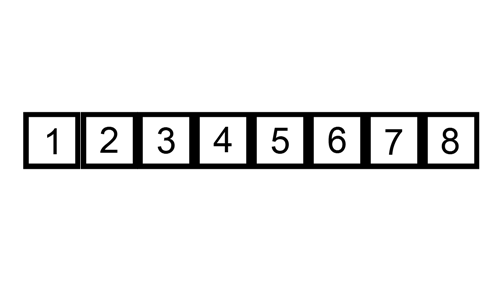
Algorithm

Step 1 - If it is the first element, it is already sorted. return 1;
Step 2 - Pick next element
Step 3 - Compare with all elements in the sorted sub-list
Step 4 - Shift all the elements in the sorted sub-list that is greater than the
         value to be sorted
Step 5 - Insert the value
Step 6 - Repeat until list is sorted

Pseudocode

procedure insertionSort( A : array of items )
   int holePosition
   int valueToInsert

   for i = 1 to length(A) inclusive do:

      /* select value to be inserted */
      valueToInsert = A[i]
      holePosition = i

      /*locate hole position for the element to be inserted */
      while holePosition > 0 and A[holePosition-1] > valueToInsert do:
         A[holePosition] = A[holePosition-1]
         holePosition = holePosition -1
      end while

      /* insert the number at hole position */
      A[holePosition] = valueToInsert

   end for
end procedure

Example Code in C#

public void InsertionSort(int[] intArray)
{
	Console.WriteLine("==Integer Array Input==");
	for (int i = 0; i < intArray.Length; i++)
	{
	    Console.WriteLine(intArray[i]);
	}

	int temp, j;
	for (int i = 1; i < intArray.Length; i++) { temp = intArray[i]; j = i - 1; while (j >= 0 && intArray[j] > temp)
		{
			intArray[j + 1] = intArray[j];
			j--;
		}
		intArray[j + 1] = temp;
	}

	Console.WriteLine("==Integer Array Output==");
	for (int i = 0; i < intArray.Length; i++)
	{
	    Console.WriteLine(intArray[i]);
	}
}

Output

==Integer Array Input==
5
6
4
3
2
1
==Integer Array Output==
1
2
3
4
5
6

Selection Sort

Key Notes
– Keeps track of “sorted” and “unsorted” index
– Looks for lowest from the “unsorted” side of array
– Swaps position with first value in the “unsorted” side
– “Sorted” side numbers are never revisited (assume it has been sorted)
– Swapping is done on the “unsorted” side only.
– Average and worst case complexities are of Ο(n²), where n is the number of items
– Inefficient sorting algorithm for large amounts of data, it is prefered for very small amounts of data

Example 1

Example 2

Algorithm

Step 1 - Set MIN to location 0
Step 2 - Search the minimum element in the list
Step 3 - Swap with value at location MIN
Step 4 - Increment MIN to point to next element
Step 5 - Repeat until list is sorted

Pseudocode

procedure selection sort
   list  : array of items
   n     : size of list

   for i = 1 to n - 1
      /* set current element as minimum*/
      min = i

      /* check the element to be minimum */
      for j = i+1 to n
         if list[j] < list[min] then
            min = j;
         end if
      end for

      /* swap the minimum element with the current element*/
      if indexMin != i  then
         swap list[min] and list[i]
      end if

   end for
end procedure

Example Code in C#

public void selectSort(int [] arr)
{
	Console.WriteLine("==Integer Array Input==");
	for (int i = 0; i < intArray.Length; i++)
	{
	    Console.WriteLine(intArray[i]);
	}

    // pos_min is short for position of min
    int pos_min,temp;

    for (int i=0; i < arr.Length-1; i++)
    {
        pos_min = i;//set pos_min to the current index of array

        for (int j=i+1; j < arr.Length; j++)
        {
            if (arr[j] < arr[pos_min])
            {
            // pos_min will keep track of the index that min is in, this is needed when a swap happens
            pos_min = j;
            }
        }

        // if pos_min no longer equals i than a smaller value must have been found, so a swap must occur
        if (pos_min != i)
        {
            temp = arr[i];
            arr[i] = arr[pos_min];
            arr[pos_min] = temp;
        }
    }

    Console.WriteLine("==Integer Array Output==");
	for (int i = 0; i < intArray.Length; i++)
	{
	    Console.WriteLine(intArray[i]);
	}
}

Output

==Integer Array Input==
5
6
4
3
2
1
==Integer Array Output==
1
2
3
4
5
6

Merge Sort

Key Notes
– Worst-case time complexity being O(n log n)

Example 1

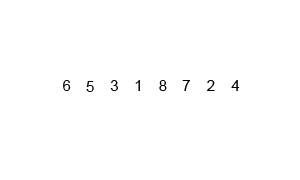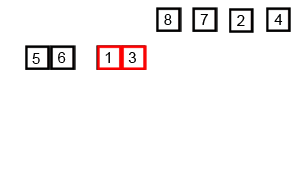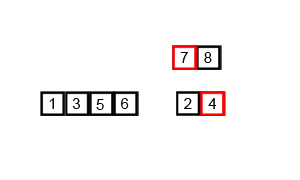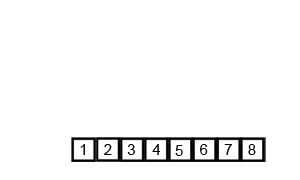
Algorithm

Step 1 - if it is only one element in the list it is already sorted, return.
Step 2 - divide the list recursively into two halves until it can no more
         be divided.
Step 3 - merge the smaller lists into new list in sorted order.

Pseudocode

procedure mergesort( var a as array )
   if ( n == 1 ) return a

   var l1 as array = a[0] ... a[n/2]
   var l2 as array = a[n/2+1] ... a[n]

   l1 = mergesort( l1 )
   l2 = mergesort( l2 )

   return merge( l1, l2 )
end procedure

procedure merge( var a as array, var b as array )

   var c as array

   while ( a and b have elements )
      if ( a[0] > b[0] )
         add b[0] to the end of c
         remove b[0] from b
      else
         add a[0] to the end of c
         remove a[0] from a
      end if
   end while

   while ( a has elements )
      add a[0] to the end of c
      remove a[0] from a
   end while

   while ( b has elements )
      add b[0] to the end of c
      remove b[0] from b
   end while

   return c
end procedure

Example Code in C#

using System;
using System.Collections.Generic;
using System.Text;

namespace CSharpSort
{
    class Program
    {
        static public void DoMerge(int [] numbers, int left, int mid, int right)
        {
            int [] temp = new int[25];
            int i, left_end, num_elements, tmp_pos;

            left_end = (mid - 1);
            tmp_pos = left;
            num_elements = (right - left + 1);

            while ((left <= left_end) && (mid <= right))
            {
                if (numbers[left] <= numbers[mid])
                    temp[tmp_pos++] = numbers[left++];
                else
                    temp[tmp_pos++] = numbers[mid++];
            }

            while (left <= left_end)
                temp[tmp_pos++] = numbers[left++];
            while (mid <= right)
                temp[tmp_pos++] = numbers[mid++];
            for (i = 0; i < num_elements; i++) { numbers[right] = temp[right]; right--; } } static public void MergeSort_Recursive(int [] numbers, int left, int right) { int mid; if (right > left)
          {
            mid = (right + left) / 2;
            MergeSort_Recursive(numbers, left, mid);
            MergeSort_Recursive(numbers, (mid + 1), right);
            DoMerge(numbers, left, (mid+1), right);
          }
        }

        static void Main(string[] args)
        {
            int[] numbers = { 3, 8, 7, 5, 2, 1, 9, 6, 4 };
            int len = 9;
            Console.WriteLine("MergeSort By Recursive Method");
            MergeSort_Recursive(numbers, 0, len - 1);
            for (int i = 0; i < 9; i++)
                Console.WriteLine(numbers[i]);
            Console.WriteLine(numbers[i]);
        }
    }
}

Output

MergeSort By Recursive Method
1
2
3
4
5
6
7
8
9
Press any key to continue . . .

Heap Sort

Example 1

Example 2

Algorithm

Note that A is an array
Step 1 BUILD-HEAP(A)
Step 2 for i = length[A], i >= 0, decrement i
Step 3 do exchange A[1]  A[i]
Step 4 heap-size[A]  heap-size[A] -1
Step 5 HEAPIFY(A, 1)

Pseudocode

l <- LEFT(i)
r <- RIGHT(i)
largest = i
if l <= heap-size[A] and A[l] > A[i]
then largest <- l
else largest <- i
if r <= heap-size[A] and A[r] > A[largest]
then largest <- r
if largest != i
then SWAP A[i] <- A[largest]
HEAPIFY(A,largest)

Example Code in C#

class Program
{
    static void Main(string[] args)
    {
        int[] arr = { 10, 64, 7, 52, 32, 18, 2, 48};
        HeapSort hs = new HeapSort();
        hs.PerformHeapSort(arr);
        Console.ReadLine();
    }
}
class HeapSort
{
    private int heapSize;

    private void BuildHeap(int[] arr)
    {
        heapSize = arr.Length-1;
        for (int i = heapSize/2; i >= 0; i--)
        {
            Heapify(arr, i);
        }
    }

    private void Swap(int[] arr, int x, int y)//function to swap elements
    {
        int temp = arr[x];
        arr[x] = arr[y];
        arr[y] = temp;
    }
    private void Heapify(int[] arr, int index)
    {
        int left = 2 * index;
        int right = 2 * index + 1;
        int largest = index;

        if (left <= heapSize && arr[left] > arr[index])
        {
            largest = left;
        }

        if (right <= heapSize && arr[right] > arr[largest])
        {
            largest = right;
        }

        if (largest != index)
        {
            Swap(arr, index, largest);
            Heapify(arr, largest);
        }
    }
    public void PerformHeapSort(int[] arr)
    {
        BuildHeap(arr);
        for (int i = arr.Length-1; i >= 0; i--)
        {
            Swap(arr, 0, i);
            heapSize--;
            Heapify(arr, 0);
        }
        DisplayArray(arr);
    }
    private void DisplayArray(int[] arr)
    {
        for (int i = 0; i < arr.Length; i++)
        { Console.Write("[{0}]", arr[i]); }
    }
}

Quick Sort

Key Notes
– Average and worst case complexity are of O(nlogn), where n is the number of items

Example 1

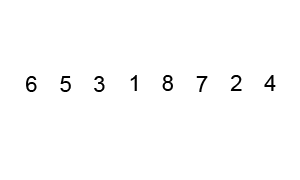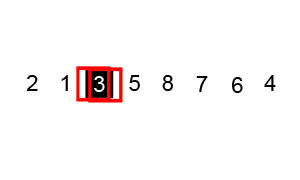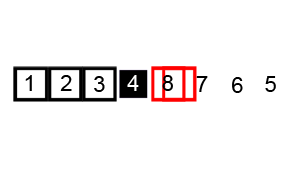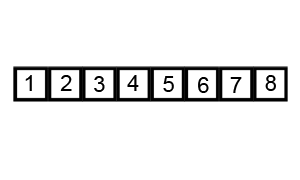
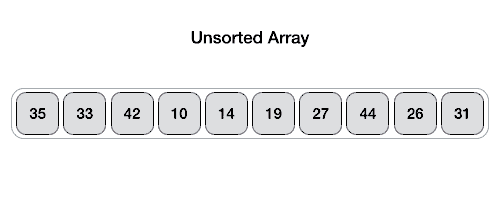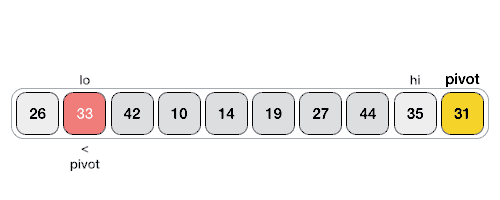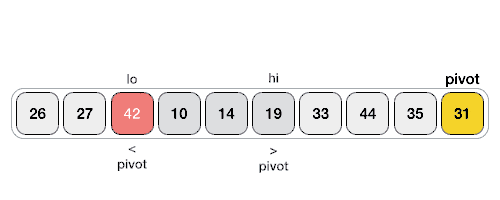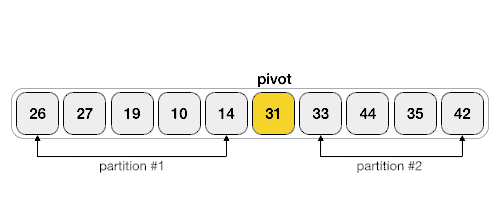
Example 2

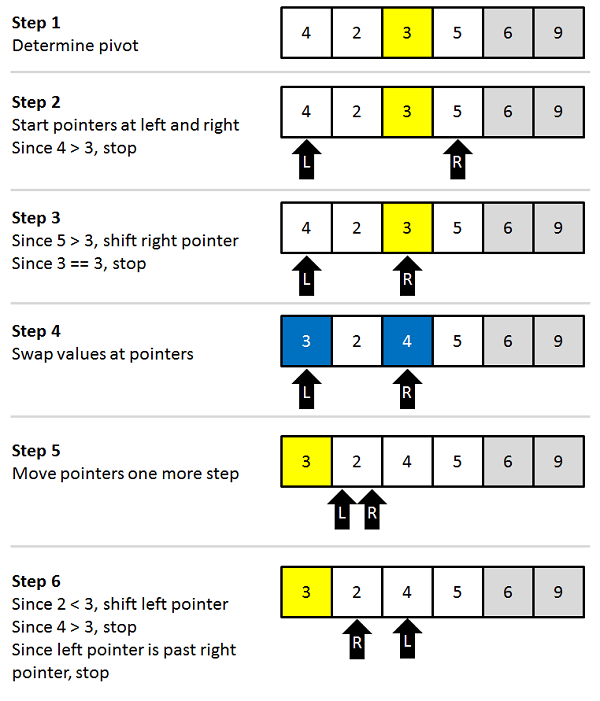
Algorithm

Step 1 - Choose the highest index value has pivot
Step 2 - Take two variables to point left and right of the list excluding pivot
Step 3 - left points to the low index
Step 4 - right points to the high
Step 5 - while value at left is less than pivot move right
Step 6 - while value at right is greater than pivot move left
Step 7 - if both step 5 and step 6 does not match swap left and right
Step 8 - if left = right, the point where they met is new pivot

Pseudocode

function partitionFunc(left, right, pivot)
   leftPointer = left -1
   rightPointer = right

   while True do
      while A[++leftPointer] < pivot do //do-nothing end while while rightPointer > 0 && A[--rightPointer] > pivot do
         //do-nothing
      end while

      if leftPointer >= rightPointer
         break
      else
         swap leftPointer,rightPointer
      end if

   end while

   swap leftPointer,right
   return leftPointer
end function

Example Code in C#

using System;
using System.Collections.Generic;
using System.Text;

namespace CSharpSort
{
    class Program
    {

        static public int Partition(int [] numbers, int left, int right)
        {
            int pivot = numbers[left];
            while (true)
            {
              while (numbers[left] < pivot) left++; while (numbers[right] > pivot)
                  right--;
               if (left < right)
               {
                  int temp = numbers[right];
                  numbers[right] = numbers[left];
                  numbers[left] = temp;
               }
               else
               {
                  return right;
               }
            }
        }

        static public void QuickSort_Recursive(int [] arr, int left, int right)
        {
            // For Recusrion
            if(left < right) { int pivot = Partition(arr, left, right); if(pivot > 1)
                    QuickSort_Recursive(arr, left, pivot - 1);
                 if(pivot + 1 < right)
                    QuickSort_Recursive(arr, pivot + 1, right);
            }
        }

        static void Main(string[] args)
        {
            int[] numbers = { 3, 8, 7, 5, 2, 1, 9, 6, 4 };
            int len = 9;

            Console.WriteLine("QuickSort By Recursive Method");
            QuickSort_Recursive(numbers, 0, len - 1);
            for (int i = 0; i < 9; i++)
                Console.WriteLine(numbers[i]);
            Console.WriteLine();
        }
    }
}

Output

QuickSort By Recursive Method
1
2
3
4
5
6
7
8
9
Press any key to continue . . .

Which Algorithm Is For Me?

It depends heavily on details of the application and implementation. The table below summarizes the important characteristics of the sort algorithms.

			Growth Rate to Srot N Items
Alorithm	Stability	Inplace	Running Time	Extra Space	Note
Insertion	Yes	Yes	Between n and n²	1	Depends on the order of the input key
Selection	No	Yes	n²	1
Bubble	Yes	Yes	n²	1
Merge	Yes	No	nlogn	n
Heap	No	Yes	nlogn	n
Quick	No	Yes	nlogn	logn	Probabilistic

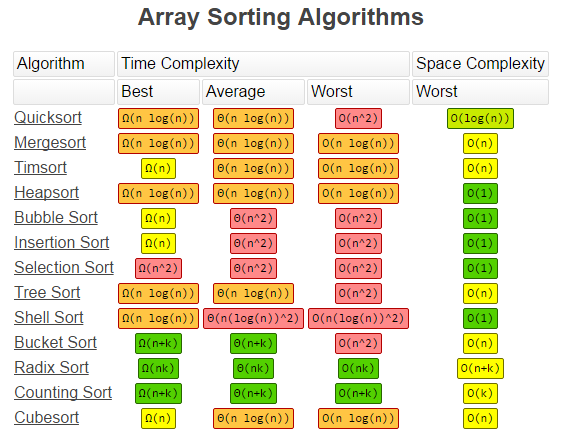
Sorting speed based on data arrangement types.

Reference

The animated GIF shown here are by no means any of my material. I got them from the website below.

M	T	W	T	F	S	S
					1	2
3	4	5	6	7	8	9
10	11	12	13	14	15	16
17	18	19	20	21	22	23
24	25	26	27	28	29	30

About the Rabi Gurung