Computers these days can perform literally millions of mathematical computations and processes in a blink of an eye, however, when a problem gets large and complicated, performance starts become a vital consideration. One of the most crucial aspects to how quickly a problem can be resolved is how the data is stored in memory.
Consider an analogy of an organized library. You can literally find the publications or books that you are looking within minutes as they are organized by title and author. Now consider the same analogy but with no organization structure, it would be days if not months until you can find your book that you are looking for.

Let’s have a quick run through basics on data types.

Primitive Data Types
In many programming language, it is also called native data types, which is essentially used to hold a single value. Example of primitive data types are boolean, integer, double, float… you get the point.
In C++, pointers are also referred to as primitive data types.

Non-Primitive Data Types
These are any data types that can be constructed in the program using programming language’s primitive data types.

• Array
• Dynamic Array Allocation
• Record (see “struct” example below)

Consider the simple example below, the “struct” declaration consist of a list of variables (members) which can be of any type.

using System;
class Program
{
    struct Simple
    {
		public int Position;
		public bool Exists;
		public double LastValue;
    };

    static void Main()
    {
		// Create struct on stack.
		Simple s;
		s.Position = 1;
		s.Exists = false;
		s.LastValue = 5.5;
		// Write struct field.
		Console.WriteLine(s.Position);
    }
}

Abstract Data Types
This data type can be explained with an analogy of a vending machine. When we use a vending machine, we insert coins into a slot, push a button, and reach into a window to take the item we selected. We don’t know how the vending machine calculates that we have given it the correct change, or how pressing a button causes an item to be made available to us.
Another all-time famous analogy would be when we are driving a car. When we get in the car, we turn the key in the ignition and the car starts. We shift into gear and drive. We don’t need to know anything about what actually happens when we turn the key to be able to drive the car.
Abstract data types serves the same function in programs, they hide unnecessary details from the user, and they allow the program designer to break up the problem into smaller more manageable pieces. I see light bulbs going everywhere.
These are typical abstract data types.

Next let’s talk about data structures.

Linear Data Structures
A data structure is said to be linear if its elements form a sequence.

• Arrays (such as array, dynamic array allocation, lookup table)
• Lists (linked list)

Tree Data Structures

• Binary trees
• Heaps
• B-trees
• Trees
• Multiway trees
• Space-partitioning trees
• Application-specific trees

Hashes Data Structures

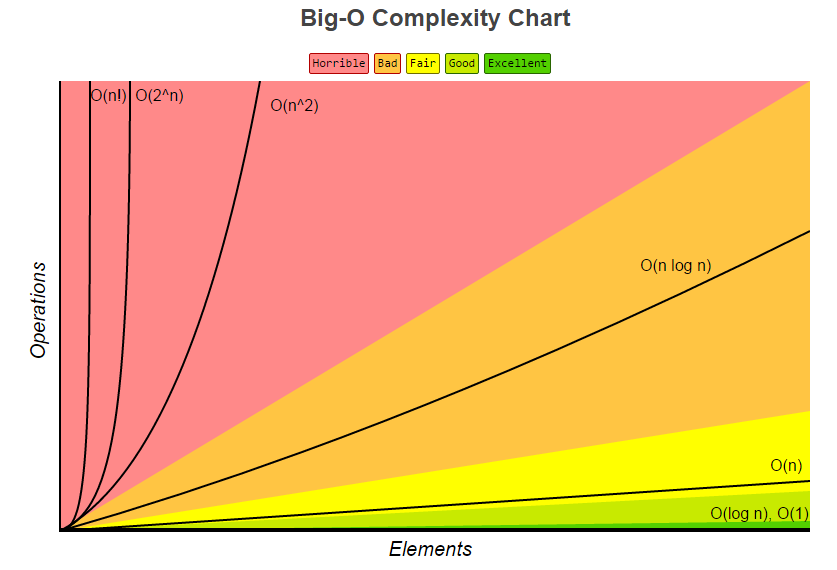
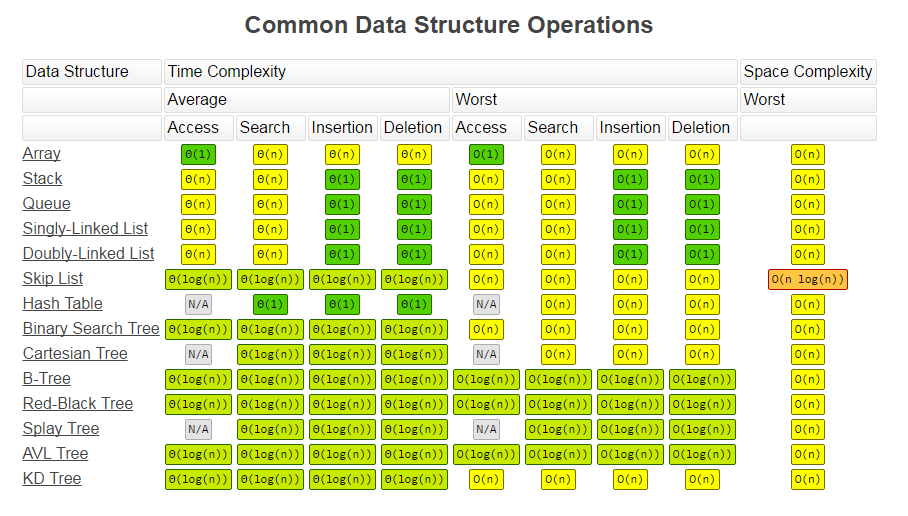
Big O Notation aka Time Complexity
Big O notation is used to describe the performance or complexity of an algorithm. That is, it specifically describes the worst-case scenario, and can be used to describe the execution time required or the space used (e.g. in memory or on disk) by an algorithm.

O(1)
O(1) describes an algorithm that will always execute in the same time (or space) regardless of the size of the input data set.

public void ReturnSongType(LinkedList elements)
{
    return elements[0] == null;
}

O(N)
O(N) describes an algorithm whose performance will grow linearly and in direct proportion to the size of the input data set.
With reference to the example below, under worst case scenario, the program will have to go through every element in the linked list to find the “petname”. For that we say the for loop ha a big O notation of O(N) where N is the maximum number of elements.

public bool LookForPet(LinkedList pets, string petname)
{
	foreach (string value in pets)
	{
		if (pets == petname) return true;
	}
}

O(N²)
O(N²) represents an algorithm whose performance is directly proportional to the square of the size of the input data set. This is commonly found in program involve nested iterations over the data set. Multi-level nested iterations will result in O(N3), O(N4) and so on.
The example below (with 2 level of nested for loop) is a good example of O(N²).

public bool LookForPetMore(LinkedList pets, string petname)
{
	foreach (string nameOuter in pets)
	{
		foreach (string nameInner in pets)
		{
			if (nameOuter == nameInner) return true;
		}
	}
}

O(2N)
O(2N) denotes an algorithm whose growth doubles with each addition to the input data set. The growth curve of an O(2N) function is exponential – starting off very shallow, then rising meteorically. An example of an O(2N) function is the recursive calculation of Fibonacci numbers.

public int Fibonacci(int number)
{
    if (number <= 1) return number;
    return Fibonacci(number - 2) + Fibonacci(number - 1);
}

O(LogN)
The iterative halving of data sets described in the binary search example produces a growth curve that peaks at the beginning and slowly flattens out as the size of the data sets increase e.g. an input data set containing 10 items takes one second to complete, a data set containing 100 items takes two seconds, and a data set containing 1000 items will take three seconds. Doubling the size of the input data set has little effect on its growth as after a single iteration of the algorithm the data set will be halved and therefore on a par with an input data set half the size. This makes algorithms like binary search extremely efficient when dealing with large data sets.
Binary search is a good example of O(LogN).

Data Structure – Linked List
A linked list is a sequence of data structures, which are connected together via links. Linked List is a sequence of links which contains items. Each link contains a connection to another link. Linked list is the second most-used data structure after array.

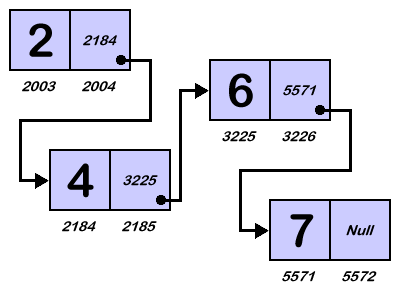
Static array uses contiguous block of memory, which works extremely well if you know the array size way in advance. However, if you don’t know the size of the array, this data structure can be especially handy as it does not employ contiguous memory allocation.
One thing to note is that in order to access, say for example the third element in the linked list, the program will have start looking from the very first element which provides the address to the second element, which provides the address to the third element.
Linked list has a time complexity of O(N).
Example of linked list in C#.

using System;
using System.Collections.Generic;
class Program
{
    static void Main()
    {
		LinkedList linked = new LinkedList();
		linked.AddLast("cat");
		linked.AddLast("dog");
		linked.AddLast("man");
		linked.AddFirst("first");
		foreach (var item in linked)
		{
		    Console.WriteLine(item);
		}
    }
}

Output:

first
cat
dog
man

Data Structure – Hash Table
A hash table is a data structure used to implement an associative array, a structure that can map keys to values. A hash table uses a hash function to compute an index into an array of buckets or slots, from which the desired value can be found.

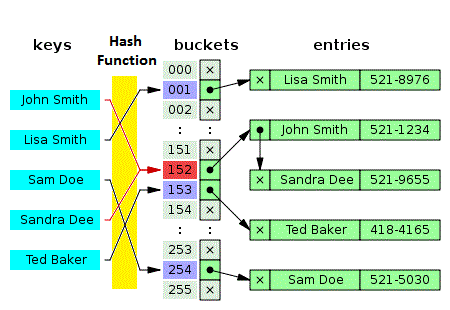
A typical hash function is h(x)=x % size of hash table.
If the Hash Function (see image above; yellow box) calculates the location to be the same for two separate element, a collision has occurred. In the example above, there is collision for data element “John Smith” and “Sandra Dee”.
These are some of the ways to resolve the collision.

There are lots of hash functions in the internet (such as extensible hashing function), but note that some are good and some are simply not effective (from time complexity basis).
The example in the diagram shows
Example of linked list in C#.

using System;
using System.Collections;
class Program
{
    static void Main()
    {
		Hashtable hashtable = new Hashtable();
		hashtable[1] = "One";
		hashtable[2] = "Two";
		hashtable[13] = "Thirteen";
		foreach (DictionaryEntry entry in hashtable)
		{
		    Console.WriteLine("{0}, {1}", entry.Key, entry.Value);
		}
    }
}

Output:

13, Thirteen
2, Two
1, One

Data Structure – Binary Tree Introduction
– Each node can have at most 2 children.
– A node with no child node is called a leaf node.
– Maximum number of nodes with tree of level x would be 2^x. For example if a binary tree has 4 levels, the maximum number of nodes that it can have is 2^4 which is 16 nodes. See image below.

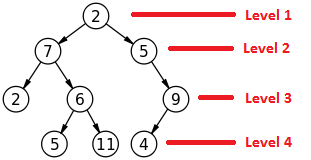
– The image below show types of binary trees. See image below.

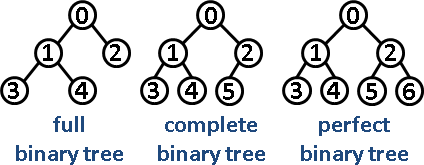
– For a binary tree to be called a Complete Binary Tree, all the nodes on the left tree must be completely filled. See image above.
– Maximum number of nodes in a binary tree with height (h) is (2^(h+1)) – 1
– Height of a complete binary tree is logN
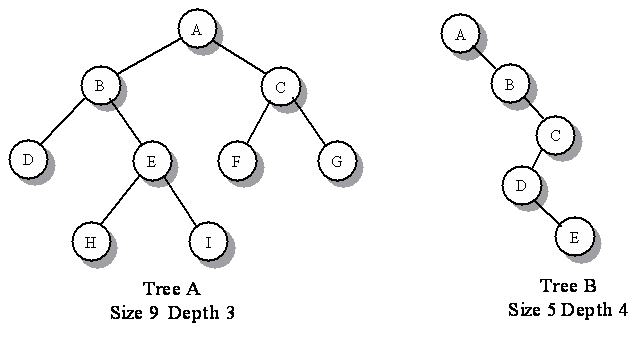
– The time complexity is proportional to the height of the tree. Therefore, it is best to reduce the height of the tree and make the tree as dense as possible (close to perfect binary tree). See image below. “Tree A” will require 3 search iterations to access element E, while “Tree B” will require 5 serach iterations.

Reference
Plenty of good materials were used to write this article, and they are as listed below.

• C# Struct
• Composite data type
• List of data structures
• Abstract data type
• Reading 8: Abstract Data Types
• Abstract Data Types
• Data Structures
• Big-O notation explained by a self-taught programmer
• A beginner’s guide to Big O notation
• LinkedList
• Know Thy Complexities!
• Introduction to linked list
• Hashtable
• Hash table
• Hashing Technique – Simplified
• Binary Tree
• Binary Trees